
De quoi dépend la perception du tempo optimal ?
Actes du colloque Le Tempo dans l'acte de performance (30-31 mars 2017), Université de Bourgogne / Conservatoire de Paris
Résumé
Pour une œuvre donnée, est-ce que les auditeurs démontrent une nette préférence pour un tempo précis, ou délimitent-ils une zone à l’intérieur de laquelle différents tempos sont tout à fait acceptables ? De quelle manière ces préférences peuvent-elles être corrélées aux différentes caractéristiques structurelles des œuvres, dans leurs groupements des phrases, leurs rythmes, leurs mélodies et leurs harmonies ? Nous avons essayé de répondre à ces questions au moyen de deux expériences différentes, toutes deux concernant des extraits de pièces baroques. Les résultats trouvés ont permis de confirmer l’existence d’un tempo préférentiel dans l’écoute des mélodies et des fourchettes de tolérance. Il a également été montré que parmi les valeurs de tempo optimal et celles de sa fourchette de tolérance, il existe une relation inverse, c’est-à-dire que les morceaux plus lents sont généralement jugés avec plus d’ambiguïté. L’analyse détaillée des différentes structures musicales qui sous-tendent les pièces en question a également permis d’identifier, au cas par cas, des tendances générales qui peuvent expliquer l’influence de différents contextes rythmique, mélodique et harmonique sur les tempos optimaux trouvés et les fourchettes de tolérance correspondantes. Le résultat le plus important nous révèle que la perception d’un tempo optimal est surtout influencée par la structure rythmique de la pièce, ainsi que, dans une moindre mesure, par d’autres éléments mélodiques et harmoniques. En particulier, nous avons trouvé que plus la densité des notes par mesure est élevée, plus le tempo préféré est lent. Nous envisageons que notre recherche puisse être utile dans les domaines de la performance et de l’éducation musicale, en permettant aux interprètes et aux étudiants de mieux comprendre les principes fondamentaux qui façonnent l’interprétation de la musique.
1. Introduction
Malgré le nombre considérable d’études qui se sont penchées sur la perception du tempo en musique (pour une revue exhaustive, voir 6. Bibliographie [28]), peu d’entre elles ont été consacrées à la question du tempo optimal, c’est-à-dire la sélection des tempos que les auditeurs percevront comme étant les plus appropriés pour la performance et le rendu expressif des pièces musicales, surtout dans le domaine de la musique classique1. Le but de cet article est de présenter les résultats de diverses expériences où ces aspects ont été abordés.
Les éléments structurels qui composent une pièce musicale (le phrasé, le rythme, le contour mélodique, la structure harmonique), tout comme l’expressivité introduite dans une performance (déviations temporelles par rapport au tempo moyen, changements de dynamique, articulation ou timbre) peut non seulement affecter la perception globale du tempo, mais également jouer un rôle crucial dans la sélection du tempo lui-même. Si un morceau est joué trop lentement ou trop rapidement, cela affectera toutes les déviations de tempo ultérieures, que les interprètes utiliseront pour accroître leur expressivité, plus particulièrement la façon dont ils décideront de mettre l’accent sur les différentes structures sous-jacentes à la pièce.
La question de l’existence d’une « vitesse » optimale pour les événements temporels qui se succèdent existe au-delà du domaine de la musique. Les études sur la vision ont démontré que la perception du mouvement dans l’espace tridimensionnel dépend de la vitesse des objets [33], que l’illusion de mouvement par les stimuli visuels successifs se produit seulement si de tels stimuli sont présentés dans une certaine plage temporelle [34], et que les participants préfèrent certains tempos plutôt que d’autres [9]. Bregman a aussi discuté des parallèles entre le mouvement apparent dans la vision et le mouvement apparent dans l’audition en termes de flux auditif2 ([8], p. 173-184).
De même, les études de Bozzi sur les pendules ont identifié certaines fréquences d’oscillation comme perceptivement « naturelles », contrairement aux lois physiques sous-jacentes [7].
À son tour, la question du tempo optimal dans la musique est considérée comme une problématique centrale à la fois dans la psychologie cognitive de la musique [1] [5] [22] [23] [25] [28] [29] [30] [31] [32] et dans la pratique de la performance expressive, et peut être motivée de la manière suivante : d’un point de vue psychologique, nous nous attendons à ce que les auditeurs concentrent leurs préférences dans une plage limitée et bien définie – des durées trop courtes entre les attaques doivent être exclues, vu l’impossibilité de relier les éléments entre eux, tandis que des durées trop longues empêchent une claire distinction des composants séparés [13] [23]. Cependant, la pratique musicale mène à des conclusions bien différentes. Comme tous les musiciens et interprètes professionnels le savent, et comme en témoignent les nombreux enregistrements d’une même œuvre – y compris celles faites par un même interprète – toutes les œuvres musicales peuvent être jouées à de nombreux tempos différents. De plus, les musiciens pratiquent des interprétations fondées sur des combinaisons spécifiques entre le tempo choisi et l’accentuation sur des structures sélectionnées.
Parmi les différentes études disponibles dans la littérature, Lapidaki (2000) a tenté d’évaluer si les auditeurs pouvaient fixer le tempo de la musique de manière cohérente. Ces études portaient sur six morceaux appartenant à différents genres musicaux (baroque, impressionniste et contemporain – musique pop et dance music), [21]. L’hypothèse était que, s’il existe des tempos privilégiés, les différents auditeurs allaient produire des réponses similaires. En utilisant la méthode d’ajustement, Lapidaki a trouvé que les sujets étaient capables d’associer à chaque morceau de musique un tempo préféré, et ces jugements étaient relativement cohérents pour la plupart des auditeurs. Toutefois, ces résultats contenaient un effet de biais lié à la familiarité avec la pièce, et ceci n’a pas permis hors de tout doute d’extraire les tempos optimaux et les caractéristiques musicales qui conduisent à de telles réponses.
D’autres études sur les performances expressives ont montré que les déviations locales du tempo sont liées à la structure réelle de la musique plutôt qu’au tempo global choisi par les interprètes [12] [30] [31], estimant que la compréhension du tempo de base est nécessaire afin de clarifier s’ils existent des tempos jugés les plus appropriés pour clarifier la structure musicale.
Dans ce contexte, Boltz (1998) a examiné si la structure d’accentuation rythmique et mélodique pouvait influencer la perception du tempo. Dans sa première étude, les auditeurs ont été invités à effectuer une tâche de comparaison de tempo par paires de stimuli. On a supposé que le nombre de changements de contours mélodiques et de sauts de hauteur impliqués dans l’écoute de la musique affectait le tempo perçu de la façon suivante : plus les changements de contours sont amples et fréquents, plus une pièce peut être perçue comme plus lente que la mélodie de comparaison. Il a été suggéré que ces changements pouvaient amener les auditeurs à percevoir des accents prolongés et des ralentissements aux points d’arrêt des phrases, et seraient augmentés ou réduits davantage par des changements réels de tempos. Ces recherches ont donné un premier aperçu des caractéristiques musicales qui affectent la perception du tempo musical par les auditeurs. Dans une seconde étude, Boltz (1998) a aussi examiné l’effet du rythme en combinaison avec des changements de hauteurs sur le tempo perçu d’une mélodie. En supposant que des rythmes compatibles et incompatibles avec la mélodie peuvent affecter autrement la perception du tempo, elle a suggéré qu’une structure rythmique qui entre en conflit avec les aspects mélodiques d’une pièce peut amener l’auditeur à se dissocier du flux anticipé du tempo, et que ce manque de cohésion peut entraîner l’auditeur à percevoir la musique de manière ambiguë.
Dans la même optique, Quinn et Watt (2006) ont exploré et identifié certains facteurs qui pourraient être en cause dans la perception de la justesse d’un tempo global donné [28]. Conformément aux études précédentes, ils ont trouvé que des auditeurs non formés musicalement peuvent avoir un jugement cohérent sur la pertinence du tempo des morceaux musicaux, en jugeant s’ils sont joués trop vite ou trop lentement. Le résultat le plus significatif est que le tempo jugé optimal varie considérablement d’une pièce à l’autre. Ces résultats ont également révélé que le rythme joue un rôle prépondérant, et – contrairement à Boltz qui avait constaté un effet de la structure mélodique sur le tempo perçu – l’absence de structure mélodique ne semble pas bloquer la capacité des auditeurs à prendre des décisions quant à la justesse du tempo. De même, les corrélations entre le tempo optimal et presque toutes les caractéristiques musicales – sauf le nombre d’intervalles décroissants – ne sont pas significatives. En particulier, aucune corrélation n’a été trouvée entre le tempo optimal et la variabilité des durées des notes ou la fréquence des notes les plus courantes.
Par le passé, dans nos propres études, nous nous étions également interrogés sur la notion du tempo optimal. Dans une première étude, nous nous étions penchés sur l’effet de l’expressivité sur les auditeurs, et nous avions trouvé qu’ils indiquaient des préférences de tempo cohérentes tout en maintenant une certaine fourchette de tolérance. L’auditeur préfère un tempo plus rapide avec une zone de tolérance plus resserrée dans une pièce dont l’indication de tempo est rapide, et un tempo plus lent avec une zone de tolérance plus large dans une pièce dont l’indication de tempo est plus lent. Lorsque le facteur de l’expressivité entre en jeu, les tempos préférés sont décalés vers des valeurs plus élevées, un effet plus accentué dans les pièces rapides [5]. Par la suite, nous avons affiné ces conclusions en corrélant la densité des éléments mélodiques avec la perception du tempo optimal dans des œuvres baroques, et démontré que même s’il existe un tempo jugé optimal, la palette de tempos jugés acceptables est tributaire de la structure rythmique. Cette palette est plus large lorsque le rythme est égal, et plus étroite lorsque le rythme est inégal. Les mélodies avec moins de notes par temps ont des tempos plus rapides, et ces tempos sont compris dans une fourchette de tolérance plus étroite ([4], BV15 dans la suite du texte).
Dans ce travail, nous reprendrons les données de BV15 et les comparerons à ceux d’une deuxième étude, assez similaire à la précédente dans sa mise en œuvre, mais faite à partir d’un extrait musical différent. En complément, nous mesurerons l’effet des différentes structures musicales sur la perception d’un tempo optimal. Nous exposerons les résultats des deux expériences : la première est la même qui a déjà été partiellement présentée dans BV15, tandis que la seconde est totalement nouvelle. Le but de ce travail est d’aller plus loin dans l’interprétation des résultats de notre première expérience, par une étude plus poussée de la relation entre le tempo optimal et les caractéristiques des structures musicales appartenant aux pièces en question – c’est-à-dire non seulement la densité des éléments mélodiques, mais aussi d’autres éléments qui interviennent dans les structures du phrasé, du rythme, de la mélodie et de l’harmonie. La combinaison de ces deux études nous permettra d’arriver à une vision plus cohérente de la relation entre la perception d’un tempo optimal dans une pièce de musique et les différentes structures sous-jacentes. Mais cela soulève une autre question de recherche : comment la perception optimale du tempo est-elle influencée par les variations expressives introduites par les interprètes ? Cette question assez vaste sera plutôt traitée dans une publication à venir.
Cet article se divise de la manière suivante. Nous commencerons par exposer les questions de recherche (point 2). Ensuite, pour chacune des deux expériences, nous décrirons la méthodologie employée : participants, extraits musicaux, déroulement de l’expérience (point 3). Puis nous donnerons les résultats, en commençant par l’analyse de la concordance entre les sujets, suivie par la détermination du tempo optimal (point 4). En continuant dans la même section, nous présenterons les analyses computationnelles des quatre pièces musicales employées, en précisant les principaux aspects qui ont été pris en compte ainsi que les algorithmes utilisés pour obtenir ces données. À la fin de la section 4, nous présenterons les résultats des corrélations entre les réponses des sujets avec les différentes structures musicales. La section 5 contient une discussion générale, notamment sur la comparaison entre les résultats quantitatifs de deux études et l’interprétation de ces résultats à la lumière de certaines intuitions musicales et des recherches précédentes. Cette section permettra de clore la question par un résumé des principaux constats que nous avons fait et de mentionner les questions qui demeurent à explorer dans des expériences ultérieures.
2. Questions de recherche
Nous cherchons à savoir si, dans une œuvre musicale, il existe un tempo global que l’auditeur perçoit comme étant optimal, et si oui, à comprendre comment il peut dépendre de la structure de la pièce et de son interprétation. Plus précisément, nous nous sommes posés deux questions :
Pour une œuvre donnée, est-ce que les auditeurs démontrent une nette préférence pour un tempo précis, ou délimitent-ils une zone à l’intérieur de laquelle différents tempos sont tout à fait acceptables ?
De quelle manière ces préférences peuvent-elles être corrélées aux différentes caractéristiques structurelles des œuvres, dans leurs groupements des phrases, leurs rythmes, leurs mélodies et leurs harmonies ?
3. Méthodologie
3.1. Première expérience
3.1.1. Sujets
18 musiciens ont participé à cette expérience : 12 hommes et 6 femmes, dont l’âge moyen est de 36,11 ans (écart de 18,18 ans) et l’expertise de 3,89 (écart de 0,68). Pour évaluer le degré d’expertise, nous avons utilisé une échelle notée de 1 à 5 : 1- non-musicien et non-amateur de musique classique; 2- non-musicien, mais amateur de musique classique; 3- musicien amateur; 4- musicien formé (étude académique de la musique depuis 10 ans), interprète ou musicologue; 5- musicien formé, interprète et musicologue. Les candidats étaient des professionnels provenant d’Italie et de Slovénie, ainsi que des étudiants du conservatoire de Trieste (Italie). Il y avait 12 pianistes, 1 flûtiste, 1 clarinettiste, 1 corniste, 1 chanteur, 1 guitariste et 1 chef d’orchestre.
3.1.2. Extraits musicaux
Pour les extraits musicaux, nous avons fait entendre les premières mesures de trois sonates de Domenico Scarlatti, correspondant à une phrase musicale complète : la sonate en fa dièse mineur, K. 25 – L. 481, mesures 1 à 12 ; la sonate en sol mineur, K. 450 – L. 338, mesures 1 à 6 ; la sonate en fa mineur, K. 238 – L. 27, mesures 1 à 5 (figure 1). Les partitions ont été transcrites à partir de l’édition de Kenneth Gilbert [18] [19] [20], adaptée en supprimant toutes les indications expressives (y compris les ornements) dans le logiciel de notation Musescore 2.13 , et puis encodée en format MIDI dans Director Musices 2.7.14 avec des sons de piano5. Les seuls ornements présents, ceux dans la sonate K. 450, ont été omis afin de ne pas altérer la structure rythmique à comparer avec celles des deux autres sonates.

Figure 1. Les trois extraits considérés dans l’expérience 1 :
sonates de Scarlatti K. 25, K. 450 et K. 238
Écouter K. 25 60 bpm 68 bpm 78 bpm 88 bpm 100 bpm 114 bpm 130 bpm
Écouter K.450 60 bpm 68 bpm 78 bpm 88 bpm 100 bpm 114 bpm 130 bpm
Écouter K.238 60 bpm 68 bpm 78 bpm 88 bpm 100 bpm 114 bpm 130 bpm
Nous avons choisi de restreindre les extraits au répertoire baroque afin de limiter la portée de l’expérience au seul paramètre de l’effet de la structure musicale sur la perception d’un tempo optimal. Bien que les trois pièces choisies aient une indication au début, à l’époque baroque, les indications de mouvement au début des pièces sont des indications générales. Comme l’explique Denis Herlin dans la préface de son édition du Premier livre de pièces de clavecin de François Couperin, publié aux éditions Bärenreiter en 2016, il y a souvent confusion entre une indication de mouvement et une indication de caractère [17]. Il appartient donc à l’interprète de choisir le tempo qui lui semble le mieux adapté pour correspondre aux indications de Couperin (ou de tout autre compositeur baroque). Cette liberté offre à l’interprète d’aujourd’hui un choix de tempo assez large – bien que dans les limites imposées par les titres qui correspondent à des mouvements de danse6 – ce qui lui permet de l’optimiser en fonction de sa manière de sentir les propriétés rythmiques, harmoniques et mélodiques de la partition. Nous avons choisi seulement des pièces en mineur parce que – vu le petit nombre de morceaux en question – nous avons décidé d’amorcer notre étude en nous concentrant sur les aspects rythmiques, en reportent les aspects harmoniques à une étape ultérieure.
Les trois extraits choisis ont d’abord été synthétisés sous forme inexpressive, c’est à dire réalisés avec un tempo métronomique et sans nuances. Pour l’ensemble des 3 extraits musicaux, 7 tempos ont été retenus à la suite d’une première évaluation faite avec un plus petit nombre de participants (incluant l’un des auteurs de l’article). Notre hypothèse était que le tempo optimal se situe plutôt au centre, près de la moyenne des 7 tempos. Les autres tempos ont été choisis selon une formule logarithmique, conformément à l’équation (1) qui suit :
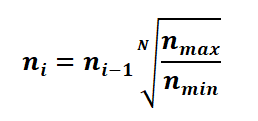
(1)
N = 6 correspond au nombre d’intervalles considérés;
i = 2,7; nmin = n1 et nmax = n7 correspondent aux tempos minimum et maximum de la série.
Le résultat de cette formule nous a donné les 7 tempos suivants : 60, 68, 78, 88, 100, 114 et 130 bpm (tempo arrondi sans les décimales).
3.1.3. Déroulement de l’expérience
Nous avons demandé aux participants de noter le degré d’optimisation du tempo selon l’échelle suivante : beaucoup trop lent, un peu trop lent, lent, mais acceptable, tempo optimal, rapide, mais acceptable, un peu trop rapide, beaucoup trop rapide (figure 2). L’appellation tempo optimal correspond au rendu qui est jugé comme étant le plus juste. Chaque extrait a été présenté en 2 blocs différents, et chaque bloc était composé de 9 essais. Chaque bloc comprenait les 7 valeurs métronomiques présentées ci-dessus, suivies de la répétition des 2 premiers essais du bloc lui-même. D’abord, l’extrait numéro 1 a été présenté dans 18 essais (9 tempos x 2 répétitions). Les 2 premiers essais de chaque répétition étaient identiques aux deux derniers ; ils ont servi à former les sujets et ont ensuite été omis de l’analyse statistique. Les deuxième et troisième morceaux ont été présentés de la même manière. Au total, il y avait 42 essais : 3 morceaux x 7 tempos x 2 blocs, plus 12 essais supplémentaires pour la formation des sujets. Tant les 7 tempos métronomiques à l’intérieur de chaque bloc que l’ordre des extraits ont été randomisés.
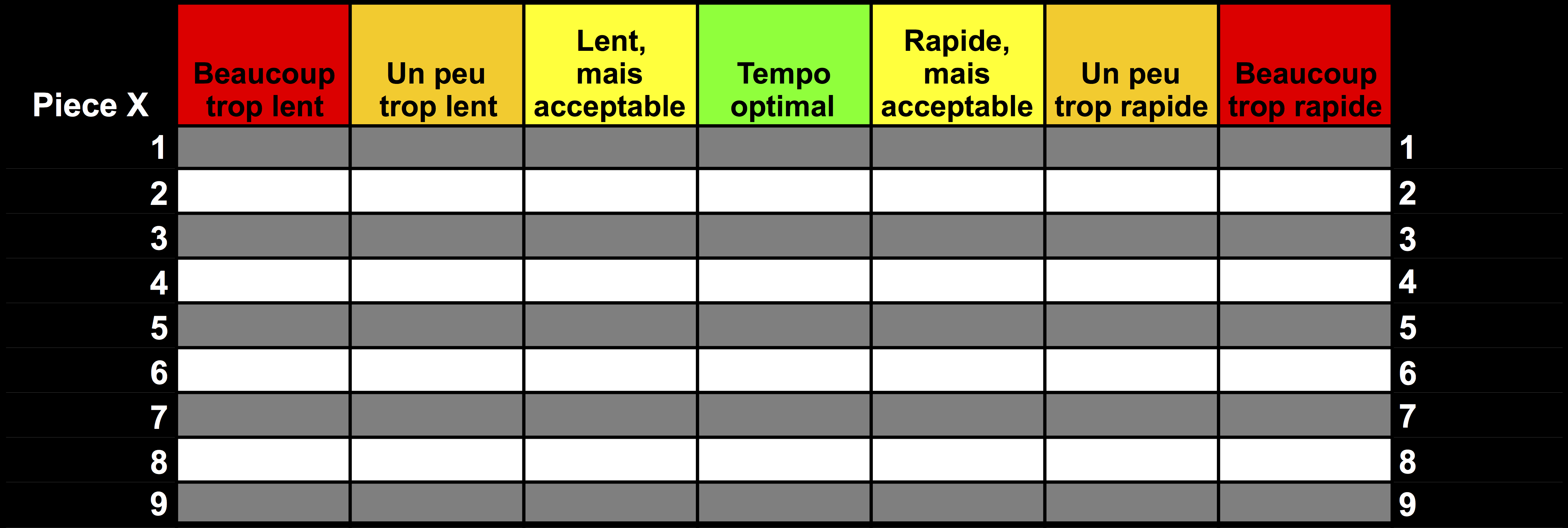
Figure 2. Grille d’évaluation distribuée aux participants.
Les choix sont compris entre « beaucoup trop lent » (en rouge/sombre à gauche) et « beaucoup trop vite » (en rouge/sombre à droite), et ils incluent les degrés intermédiaires : lent, mais acceptable ; rapide, mais acceptable (en jaune/clair) ; un peu trop lent et un peu trop vite (en orange) ; tempo optimal (en vert au centre).
Au commencement de l’expérience, les sujets ont signé un formulaire de consentement contenant un résumé de la tâche à accomplir, précisant que cette tâche ne comportait aucun risque ni situation inconfortable, stipulant que les résultats seraient anonymes et mentionnant qu’ils pouvaient en tout temps se retirer de l’expérience, voire demander à ce que leurs résultats soient retirés7. Après l’expérience, les participants ont été soumis à un questionnaire où ils ont précisé leur âge, leur genre, leurs antécédents musicaux (selon l’échelle présentée au point 3.1.1.), leur nationalité, les stratégies mentales adoptées pour répondre aux questions, ainsi que les difficultés traversées au cours de l’expérience. Enfin, nous avons demandé aux sujets leur degré de familiarité avec les stimuli. La réponse a été, en moyenne, le manque de familiarité avec les pièces en question, compensé toutefois par une certaine familiarité avec leur genre. La durée totale de toutes ces étapes était d’environ 45 minutes.
3.2. Deuxième expérience
3.2.1. Sujets
18 musiciens y ont participé : 12 hommes et 6 femmes, dont l’âge moyen est de 30,29 ans (écart de 9,80 ans) et l’expertise de 4,11 (écart de 0,76). Les critères pour évaluer l’expertise des candidats étaient les mêmes que pour la première expérience. Ceux-ci étaient des professionnels et des étudiants de l’Université de Montréal provenant du Canada, des États-Unis, de la France et de la Chine. Il y avait 6 pianistes, 2 guitaristes jazz, 1 guitariste classique, 2 violonistes, 2 chanteurs, 1 flûtiste, 1 organiste, 1 bassiste, 1 contrebassiste et 1 percussionniste.
3.2.2. Extrait musical
Cette deuxième expérience sur la perception du tempo optimal était elle aussi basée sur un extrait du répertoire baroque, soit le premier Prélude de L’Art de toucher le clavecin de François Couperin, pour une phrase qui correspond aux mesures 9 à 16 (figure 3). La partition a été transcrite et adaptée dans Finale 2014.58 d’après le fac-similé de l’édition de 1716 du Sieur Foucaut [11]. Depuis Finale, une version a été sauvegardée en format XML et transformée en format MIDI. Un fichier sonore en format WAV a été généré depuis Finale, avec le son de clavecin du Garritan Personal Orchestra 4.09, pour produire des interprétations métronomiques. Les tempos utilisés étaient les mêmes que ceux de l’expérience 1, soit 60, 68, 78, 88, 100 114 et 130 bpm à la noire10.

Figure 3. François Couperin : premier Prélude, tiré de L’Art de toucher le clavecin, mes. 9 à 16
(utilisé pour les expériences 2 et 3)
Écouter l'extrait : 60 bpm 68 bpm 78 bpm 88 bpm 100 bpm 114 bpm 130 bpm
3.2.3. Déroulement
Le déroulement était le même que pour l’expérience 1, à la différence que les participants n’ont reçu qu’une seule série d’essais sonores. Contrairement à l’expérience précédente, les sujets ne disaient qu’ils ne connaissaient généralement pas la pièce entendue.
4. Résultats
4.1 Analyse statistique des données
Les résultats des deux expériences sont présentés à la figure 4, dont chaque courbe montre les moyennes et les écarts-types sur les tempos assignés pour chacun des 7 tempos métronomiques fournis à titre d’essai. Les résultats pour chaque expérience sont affichés séparément. Sur l’axe vertical, les points correspondent aux descripteurs selon la règle présentée précédemment : -3 = « extrêmement lent » ; -2 = « un peu trop lent » ; -1 = « lent, mais acceptable » ; 0 = « tempo optimal » ; 1 = « rapide, mais acceptable » ; 2 = « un peu trop rapide » ; 3 = « extrêmement rapide ». Sur l’axe horizontal, les nombres correspondent aux sept tempos métronomiques énumérés ci-dessus (classés par ordre croissant). Les barres verticales indiquent un indice de fiabilité de 95 %. Pour tester notre hypothèse sur l’influence du tempo métronomique sur les évaluations des sujets, nous avons effectué l’analyse de la variance à mesures répétées à trois voies pour l’expérience 111 (facteurs : Pièce, Répétition et Tempo) et l’analyse de la variance à mesures répétées à deux voies pour l’expérience 2 (facteurs : Pièce et Tempo). Notre analyse montre que, dans l’expérience 1, les facteurs Pièce, Tempo, et les interactions Pièce x Tempo et Pièce x Répétition x Tempo sont significatifs (p < 0,05). Dans l’expérience 2, le seul facteur Tempo est aussi significatif (p < 0,001). Dans l’expérience 1, la pièce 1 (Scarlatti sonate K. 25) a été évaluée plus lentement que la pièce 2 (Scarlatti, sonate K. 450) et la pièce 2 plus lentement que la pièce 3 (Scarlatti, sonate K. 238), et cela arrive dans chaque tempo présenté. En passant de tempos plus lents à des tempos plus rapides, les différences entre les trois morceaux deviennent de plus en plus petites. Dans l’expérience 2, la pièce 4 (prélude de Couperin) a été évaluée approximativement comme la pièce 1 (sonate K. 25) aux tempos plus lents et converge vers les évaluations moyennes des sonates K. 450 et K. 238 aux tempos plus rapides.
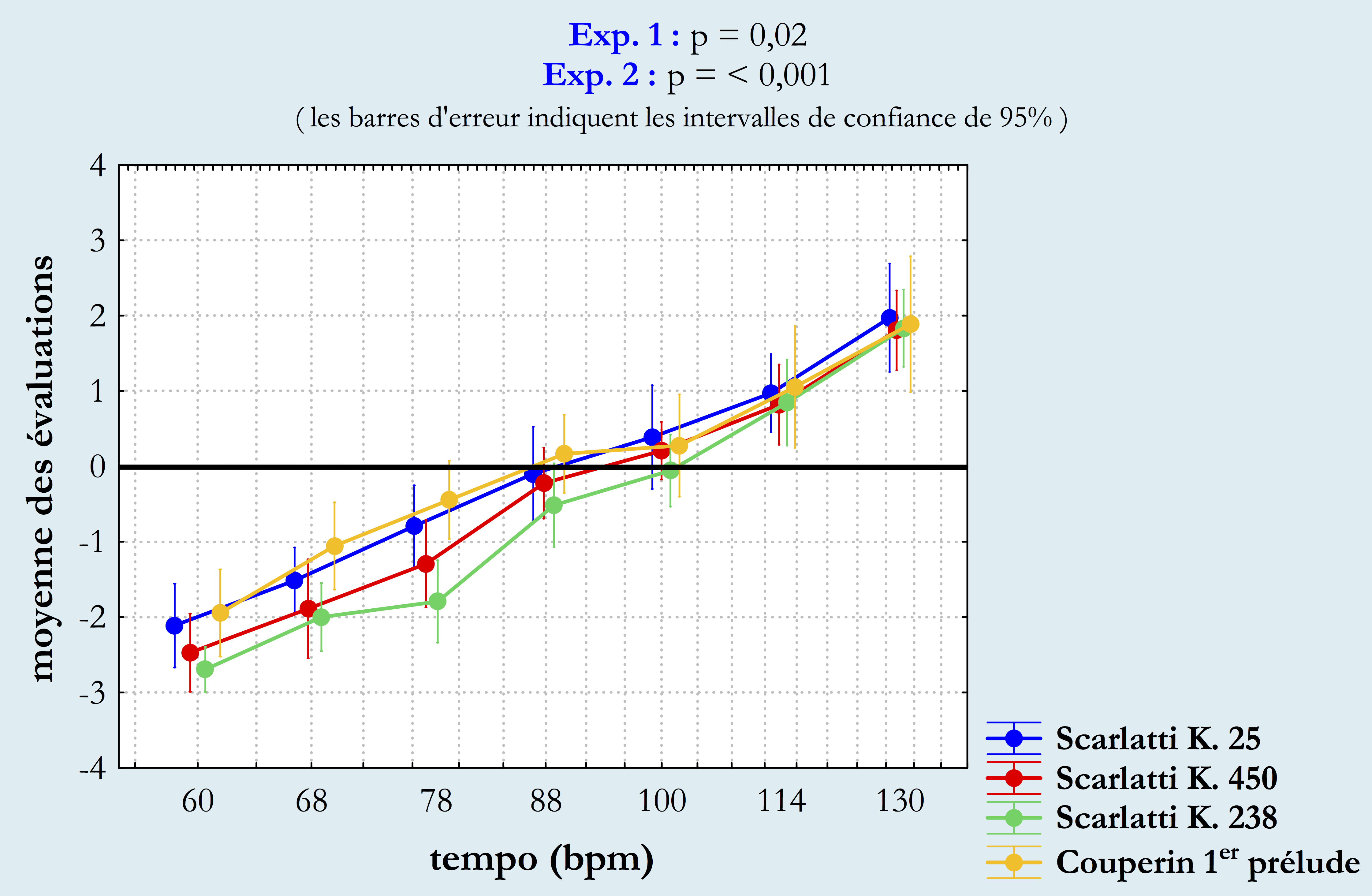
Figure 4
Moyenne des évaluations pour les pièces considérées dans BV15 et dans notre deuxième expérience.
Les barres d’erreur indiquent les erreurs sur les moyennes en tenant compte des effets d’interaction au sein d’une même expérience. Dans le cas du prélude de Couperin, les indications métronomiques sont à la noire. Une ligne horizontale a été dessinée à l’endroit correspondant au niveau du tempo optimal.
4.2 Détermination du tempo optimal
À partir des résultats représentés dans la figure 4, les tempos optimaux pour chaque pièce ont été obtenus au moyen des régressions linéaires, en cherchant les zéros comme points d’intersection entre les courbes et les axes des x. Les résultats sont présentés dans le tableau 1. Ici, la signification des différents paramètres est la suivante : A est la pente de la droite d’interpolation entre les sept points, B est l’intercepte avec l’axe vertical, sA et sB sont respectivement les incertitudes sur A et B, r est le coefficient de corrélation qui mesure la fiabilité de l’ajustement, et p donne une mesure de sa significativité.
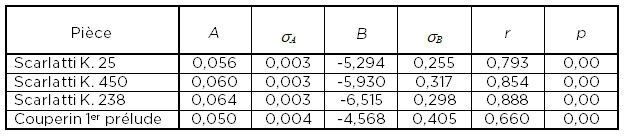
Tableau 1. Résultats des régressions linéaires pour les quatre pièces utilisées dans nos études
Comme on peut le voir, tous les quatre ajustements présentent un niveau de signification très élevé (p < 0,001). Cependant, il faut souligner que la qualité de l’ajustement pour les trois premières pièces, celles correspondant à l’expérience 1, est beaucoup plus élevée que pour la pièce présentée dans l’expérience 2, comme il résulte des valeurs très différentes du coefficient de corrélation r. Ceci est la conséquence d’une plus grande variabilité entre les sujets lors de la seconde expérience et met en évidence l’utilisation de différentes stratégies entre les deux groupes. Compte tenu des tendances générales expliquées ci-dessus et de ces premiers résultats, nous avons décidé d’explorer plus en détail les différences entre les quatre pièces.
Donc, nous avons effectué le test F pour les variances pour chaque paire de pièces (xi, xj), i, j = 1,4, afin de vérifier si l’hypothèse nulle indiquant que l’écart-type pour la population de la pièce xi peut être considérée égale à l’écart-type de la population de la pièce xj. En d’autres termes, nous avons testé si la différence entre les écarts-types des populations pour chaque paire de pièces différentes n’était pas suffisamment importante pour être statistiquement significative. Le but de ce test était de comparer les deux groupes de sujets en termes de cohérence entre leurs réponses. Les résultats sont résumés dans le tableau 2. Bien que l’hypothèse nulle puisse être rejetée pour les variances globales de toutes les paires (non indiquées dans le tableau), il y a des différences significatives entre les groupes si on regarde les 7 tempos séparément. Comme on peut le voir, ces différences sont plus nombreuses pour deux des trois paires obtenues en combinant les expériences 1 et 2 (c’est-à-dire, pour les paires 2-4 et 3-4). Ceci indique que la cohérence entre les deux groupes de participants impliqués dans les deux études était différente (pire dans l’expérience 2 par rapport à l’expérience 1). Autrement, à l’intérieur du premier groupe de sujets les évaluations étaient plus cohérentes, malgré les différences structurelles entre les trois pièces. Fait intéressant, la différence entre les deux groupes de sujets est très faible (n’impliquant qu’un seul tempo) lorsque l’on compare les pièces 1 et 4. Comme ces deux pièces ont une figuration rythmique et une densité de notes similaires (voir les figures 1 et 3), cela pourrait être considéré comme une première indication de l’effet de la structure musicale sur les évaluations du tempo. Dans tous les cas, nous remarquons que les différences significatives concernent en général les tempi qui sont situés aux extrémités inférieure et supérieure de la fourchette (c'est-à-dire, trop lent ou trop rapide).
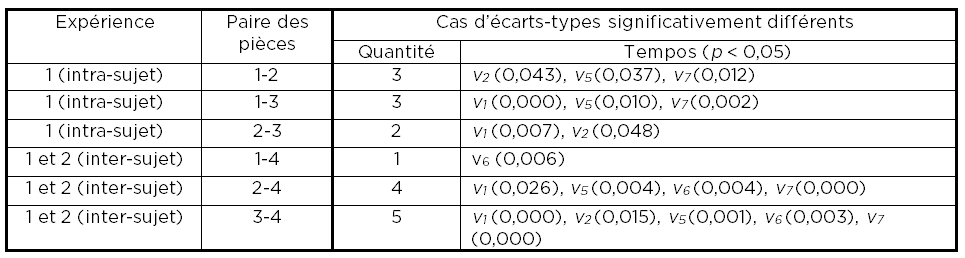
Tableau 2. Test F pour les variances entre les différentes expériences et paires de pièces
Malgré le niveau d’expertise plus élevé du deuxième groupe, une analyse minutieuse des débriefings nous a permis d’esquisser une interprétation des raisons pour lesquelles les deux études ont produits des variabilités différentes. À la question « Avez-vous rencontré des difficultés lors de la tâche ? », le premier groupe de sujets a donné des réponses presque toujours positives, en insistant en particulier sur la difficulté à donner des réponses cohérentes entre les différents stimuli présentés et l’inconfort produit par le manque d’expressivité dans les échantillons. En fait, à la question suivante : « Quelles stratégies mentales avez-vous suivies dans l’attribution des évaluations ? », les réponses des sujets portaient beaucoup sur les aspects structurels des pièces, cherchant des motivations rationnelles pour leurs choix qui s’appuient sur leur connaissance de la théorie musicale, leur affinité avec des morceaux similaires à ceux présentés, mais qui leur étaient mieux connus, ou leur expérience d’interprètes. En revanche, dans les deux questions, les sujets du groupe 2 ont souvent donné des réponses plus vagues, faisant généralement appel à l’intuition et au goût personnel plutôt qu’à l’expérience. Donc, nous interprétons la majeure variabilité dans le groupe 2 comme un effet d’un niveau de concentration plus faible dans la réalisation de la tâche, ou d’une moindre connaissance du répertoire en question (alors qu’ils avaient un niveau d’expertise générale en musique plus élevé).
Une fois que les lignes de régression ont été déterminées, il était possible d’extraire les tempos optimaux et les respectifs écarts-types par une procédure d’interpolation sur l’échelle de temps exprimée par l’équation 1. Les résultats sont indiqués dans le tableau 3.
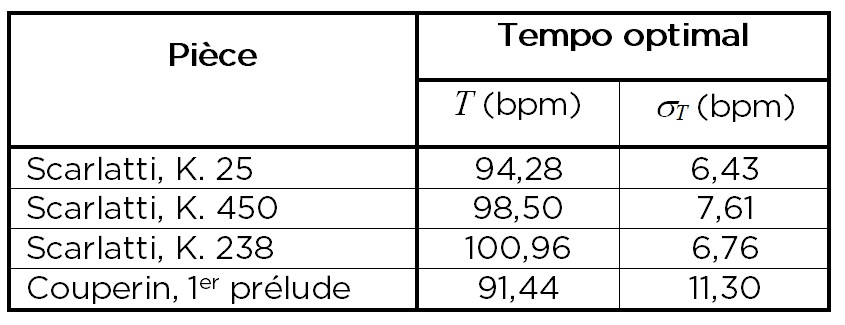
Tableau 3. Les tempos optimaux (en bpm) et leurs écarts-types
Nous concluons cette première partie de notre analyse en disant que pour chacune des quatre pièces prises en compte, il n’y a qu’un et un seul tempo préférentiel, auquel est associée une certaine plage de tolérance. Dans la figure 4, le tempo préférentiel est déterminé à partir de l’intersection de la ligne droite qui se rapproche le mieux des données mesurées avec l’axe des x, tandis que l’intervalle de tolérance correspond à la région comprise entre les jugements « lent, mais acceptable » et « rapide, mais acceptable » qui correspondent aux valeurs -1 et 1 sur l’axe vertical. Pour le quatrième morceau, c’est-à-dire le prélude de Couperin, la plage de tolérance est plutôt élevée : cela signifie un degré plus haut d’indétermination sur le tempo optimal. Pour les trois autres pièces (sonates de Scarlatti), les temps optimaux peuvent être déterminés avec une plus grande précision. Cependant, comme nous l’avons déjà signalé ci-dessus, leurs valeurs diffèrent entre eux, et il y a une certaine proximité dans les valeurs de tempo optimal entre la sonate K. 25 de Scarlatti et le prélude de Couperin. La deuxième partie de notre analyse a donc été consacrée à l’exploration de cette mise en relation : comment les différentes structures musicales qui interviennent pour caractériser chaque pièce peuvent être en partie responsables de ces tendances ?
4.3 Analyse structurelle des pièces
Pour caractériser les différentes pièces, les structures suivantes ont été prises en compte : densité (nombre de notes par mesure), durée des notes (écart-type), complexité de la représentation rythmique, longueur des regroupements principaux, tension métrique, tension de syncope, extension du registre mélodique, taille moyenne des intervalles (moyenne et écart-type), direction moyenne des intervalles, quantité des intervalles ascendants et descendants (en pourcentage), tension mélodique, dissonance harmonique, changements de note fondamentale (root change), tension harmonique. Pour certains de ces paramètres, nous avons utilisé des modèles développés par nous-mêmes, que nous illustrerons brièvement ci-dessous.
Complexité de la figuration rythmique. Trois aspects ont été pris en compte et regroupés : la variance entre les durées des notes, à la fois dans chaque temps et entre deux temps consécutifs, l’amplitude globale de l’effet produit par les syncopes (le cas échéant), et la polyrythmie (cet aspect est toutefois absent de notre répertoire). En ce qui concerne le deuxième élément – la contribution à la complexité rythmique produite par les syncopes – notre modèle comprend deux volets simultanés : (i) l’effet global des syncopes tout au long de la pièce, et (ii) la saillance moyenne des notes syncopées. Pour chacun de ces aspects, nous avons attribué un poids total de 50%. À son tour, l’effet global de la syncope tout au long de la pièce est la somme de deux sous-effets : (i) le nombre moyen de syncopes par mesure (avec une contribution relative de 40%) et (ii) le nombre moyen de voix syncopées (contribution relative de 10%). Le degré d’importance moyen des notes syncopées est obtenu en comparant la durée d’une note avec la durée de la note précédente. Deux cas ont été considérés : si la note précédente appartient à la même voix (rythme individuel), et si la note précédente correspond à l’attaque précédente (le rythme résultant, qui représente la somme rythmique de toutes les voix). Pour chacun de ces deux cas, l’importance, ou saillance, de chaque note syncopée est obtenue par le rapport entre la durée de la note précédente et la durée de la syncope : plus une syncope est longue, plus sa saillance est faible. Les deux valeurs résultantes sont ensuite moyennées. Si le rythme est régulier, la durée de la note précédente se rapproche de l’unité de tempo, alors la saillance de la syncope est une mesure de la déviation du rythme syncopé par rapport au rythme global. Plus le rythme est irrégulier, plus l’effet de syncope est local (cf. aussi [10]).
Tensions groupale, métrique, de syncope, mélodique et harmonique. Pour déterminer les facteurs qui contribuent à construire la tension de la pièce, impliquant des aspects rythmiques, mélodiques, et harmoniques, nous avons été inspirés par la théorie des accents développée par Bisesi, Friberg et Parncutt [2] [3] [15]. Selon Bisesi et coll., les « accents musicaux » sont des éléments musicaux capables d’attirer l’attention de l’auditeur en donnant la sensation de ce qui est important dans la partition ; de cette façon, ils clarifient la forme et facilitent la communication musicale. En principe, ils se divisent en deux catégories principales : les accents encodés, qui sont ceux qui appartiennent à la partition, et les accents interprétés, qui sont attribués au son par les interprètes au moyen des attributs perceptifs principaux dans la musique – c’est-à-dire les déviations locales de tempo (accelerando et rallentando), de la nuance (crescendo et diminuendo), de l’articulation (legato et staccato) et du timbre. Puisque toutes les pièces utilisées dans cette étude sont des exécutions métronomiques de la partition qui ne contiennent donc pas de variations expressives, nous parlerons toujours des accents encodés dans la suite du texte. Par ailleurs, toujours selon Bisesi et coll., les accents encodés se classent en quatre types : le phrasé (accents groupaux, indiqués par un G), la métrique (M), les contours mélodiques (C) et l’harmonie (H) [3] [26]. En plus de ces quatre typologies, nous proposons ici une cinquième catégorie – celle des accents rythmiques de syncope (S).
Les accents groupaux sont déterminés intuitivement au début et à la fin de chaque phrase. Selon une première estimation, leur saillance, ou degré d’importance, correspond au degré hiérarchique auquel un élément va appartenir pour commencer ou terminer une phrase. Les regroupements hiérarchiques principaux sont déterminés au moyen d’une analyse manuelle basée sur notre intuition – différemment des quatre autres types d’accent, dont la détermination et l’évaluation sont automatisées. Les accents métriques traduisent simplement le mètre et la mesure indiquée dans la partition, avec ses temps forts et ses temps faibles, et leur saillance peut être estimée en considérant les différents niveaux de pulsation auxquels ils appartiennent et en ajoutant les saillances de tous les niveaux métriques marqués sur chaque note. Les accents de contours mélodiques surviennent à des sommets ou à des creux locaux, ainsi que lors de sauts mélodiques. Les accents harmoniques peuvent se produire lors d’événements avec des changements de tension harmonique, tels que les sommets ou les résolutions harmoniques, et comprennent des dissonances et des changements harmoniques (accords et modulations ou changements surprenants de la fondamentale). Chacun de ces deux derniers types d’accent – mélodiques et harmoniques – est défini à partir des combinaisons linéaires de deux entités distinctes : l’étendue du saut mélodique qui précède la note et la distance de la note accentuée par rapport à l’ambitus moyen de la mélodie dans le cas des accents mélodiques, et l’ampleur de la dissonance et de la force du changement harmonique dans le cas des accents harmoniques. Pour une description détaillée des algorithmes utilisés pour estimer la saillance des accents métriques, mélodiques et harmoniques, voir [2]. Enfin, les accents de syncope sont définis à partir de la seconde contribution au modèle pour la complexité de la figuration rythmique présentée ci-dessus, où la saillance des notes syncopées est obtenue par le rapport entre la durée de la note précédente et la durée de la syncope (voir également [10]).
À partir de ces modèles, dont le but est de sélectionner les notes les plus importantes dans une partition en fonction de leur rôle musical, il devient possible – en utilisant les mêmes algorithmes – d’en faire une extension qui permette d’extraire les tensions associées à chaque note de la pièce. En ce qui concerne les tensions mélodiques et harmoniques, il ne s’agit plus de choisir seulement un nombre limité de notes importantes, mais de les considérer toutes, et d’évaluer la contribution moyenne de leurs tensions sur la pièce. Dans cette étude, le paramètre que nous avons pris en considération pour caractériser la tension groupale est la longueur moyenne des regroupements hiérarchiques principaux. En plus, les tensions métriques et de syncope sont bien obtenues à partir de la moyenne des valeurs de saillance respectives.
À titre d’exemple, la figure 5 montre un exemple de calcul au niveau local des accentuations groupales, métriques, de syncope, mélodiques et harmoniques, avec leurs tensions associées, pour l’une des quatre pièces qui nous avons pris en compte : le prélude de Couperin. Dans la figure, les accents métriques traduisent simplement la métrique en 2/2 : les notes à la noire sont regroupées pour former une impulsion de quatre quarts par mesure. Le premier accent mélodique se trouve à la mesure 11 (fa 4) : il correspond à la distance franchie par le saut mélodique et le précède de manière à attirer l’attention. L’accent mélodique au milieu de la mesure 13 (sol 4) possède un haut degré de saillance parce qu’il y a à la fois un grand saut (7e majeure) et une grande déviation par rapport à la hauteur moyenne de la mélodie. L’accent au milieu de la mesure 12 (fa 3) correspond à un creux mélodique. Dans cette pièce, les accents harmoniques proviennent essentiellement du changement de position des accords et des altérations liées aux mouvements de la basse. L’accent harmonique au début de la mesure 11 est plus fort que les autres parce qu’il correspond à un changement important de la fondamentale, tandis que les accents et les tensions dans la mesure 13 sont une conséquence du changement du mode, du mineur au majeur, créant ainsi une grande tension harmonique. L’accent harmonique le plus important, enfin, se trouve à la cadence finale.
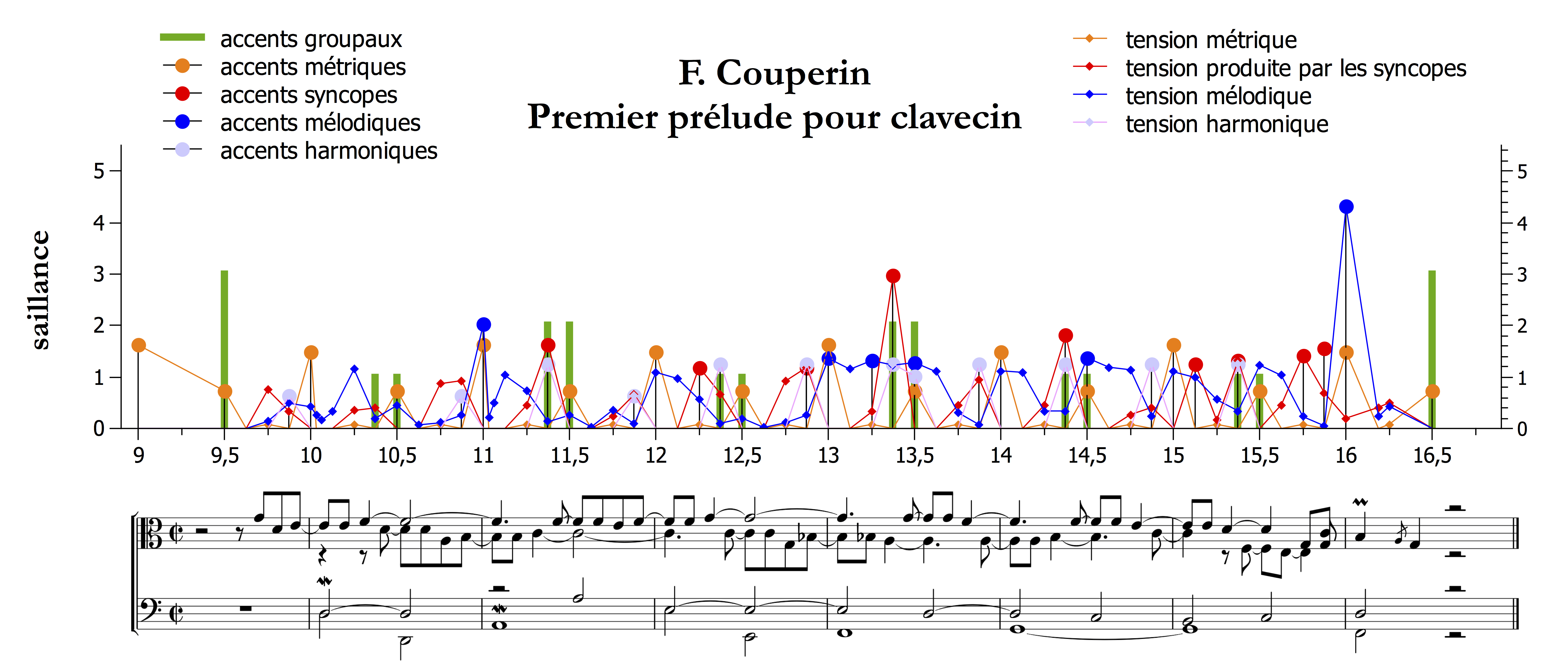
Figure 5. Exemple d’évaluation computationnelle des différentes contributions à l’accentuation et à la tension
pour le premier Prélude de Couperin.
Le diagramme de Kiviat de la figure 6 montre une comparaison résumée entre les différents morceaux en termes de tous les paramètres structurels que nous avons choisis pour les caractériser. Dans la partie supérieure nous avons représenté, dans une échelle logarithmique de base 2 pour tous les paramètres en considération, les six paramètres liés aux structures hiérarchiques de phrasé, rythme et mètre – selon les prédictions de nos modèles illustrés ci-dessus. Dans la partie inférieure, nous avons illustré les calculs relatifs aux structures mélodiques et harmoniques. Au-delà des contributions aux tensions respectives, l’amplitude du registre mélodique et les propriétés des intervalles ont également été prises en compte. Pour obtenir les données de la figure 6, chaque paramètre a d’abord été estimé localement (selon le cas, au niveau des attaques des notes ou des tactus ; voir la description ci-dessus), puis moyenné tout au long de la pièce. L’avantage de ce type de graphique est de permettre une comparaison directe entre les différentes pièces. A titre d’exemple, nous observons comment l’écart-type dans la durée des notes diffère progressivement entre les trois pièces de Scarlatti, et celui de Couperin présente une valeur non négligeable puisque les ornements y ont été pris en compte. La complexité rythmique est plus élevée dans la sonate K. 238 de Scarlatti – à la suite de la figuration avec les notes pointées, et dans la pièce de Couperin – en raison des nombreuses syncopes (dont l’effet global est également enregistré dans le même graphique). En ce qui concerne les structures mélodico-harmoniques, les différences principales sont observées dans la taille moyenne des intervalles et le changement de fondamentale, dont la contribution produite par les notes de passage dissonantes de courte durée est, avec la dissonance, responsable de la sensation perceptuelle d’une plus grande tension harmonique. Comme on peut le constater, le choix des pièces est suffisamment différencié pour faire face à une analyse des corrélations entre les différents paramètres et le temps optimal.
Figure 6. Comparaison entre les quatre pièces selon leur paramétrisation structurelle
(pour de touts les paramètres, représentation donnée dans une échelle logarithmique de base 2).
Pour permettre la représentation sur une échelle logarithmique, la direction moyenne des intervalles dans la figure a été rééchelonnée de [-1;1] à [0;2].
4.4 Analyse des dépendances du tempo optimal de la structure musicale
Après avoir caractérisé les morceaux au moyen de leurs structures, nous avons ensuite recherché les corrélations entre les tempos optimaux et leurs écarts-types, que nous avons prédits à partir des régressions linéaires illustrées dans les tableaux 1 et 3, et toutes les paramètres proposés ci-dessus. Les résultats sont donnés dans le tableau 412.
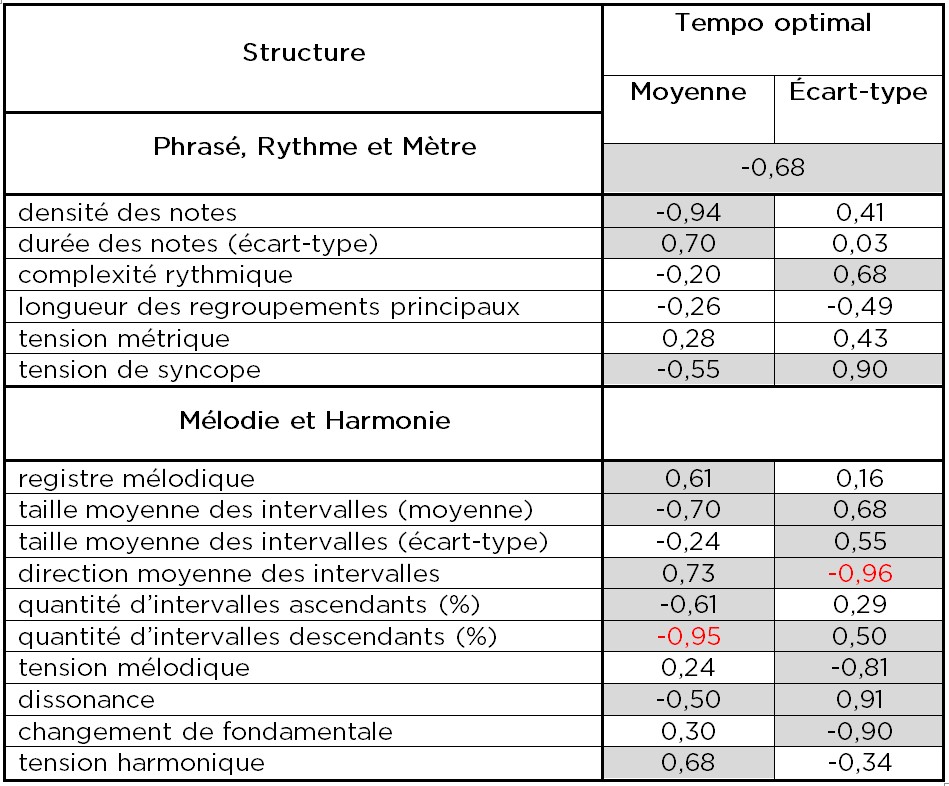
Tableau 4. Coefficients de corrélation linéaire entre les différentes structures musicales et les tempos optimaux pour l’ensemble des quatre pièces étudiées
Les corrélations significatives (p < 0,05) sont indiquées en rouge.
En raison du nombre limité de pièces étudiées, nous n’avons obtenu que deux corrélations significatives (p < 0,05). Cependant, nous rapportons également les autres valeurs, que nous interprétons comme des indications de tendance. Si elles sont supérieures à 0,5 (ou inferieurs a -0,5), les cases correspondantes sont grisées. Une interprétation de ces résultats sera abordée dans la section suivante.
5. Discussion et conclusions
Les résultats trouvés nous ont permis de confirmer l’existence, déjà démontrée dans des recherches antérieures [5] [6] [21] [23] [25] [28] [35], d’un tempo préférentiel et des fourchettes de tolérance dans l’écoute des pièces. Comme les sujets ont écouté les stimuli dans un ordre aléatoire, nous excluons que nos résultats puissent être biaisés par un effet de mémorisation. L’analyse détaillée des différentes structures musicales qui sous-tendent les pièces en question a également permis d’identifier, au cas par cas, des tendances générales qui peuvent expliquer l’influence de différents contextes rythmiques, mélodiques et harmoniques sur les tempos optimaux trouvés et les fourchettes de tolérance relatives. Compte tenu du nombre limité de pièces en question, nous voudrions souligner que toutes les considérations qui suivent se rapportent aux tendances observées, dont la généralisation nécessiterait d’étendre la présente étude à un répertoire beaucoup plus vaste. Parmi ces tendances, nous avons trouvé que plus la densité des notes par mesure est élevée, plus le tempo préféré est lent. Pour interpréter ces résultats, nous nous appuyons sur les études réalisées par Fraisse et London concernant le rythme et le mètre [13] [23]. Selon Justin London :
« Ce ne sont pas tous les stimuli périodiques qui permettent [de créer] le mouvement – certains sont trop rapides, d’autres sont trop lents. Des lumières qui clignotent rapidement peuvent devenir floues, et des robinets qui s’égouttent lentement (mais régulièrement) vont nous empêcher de prévoir quand la prochaine goutte va tomber… La limite inférieure du mètre, c’est-à-dire l’intervalle le plus court que nous pouvons entendre ou performer comme élément de la figure rythmique, est d’environ 100 millisecondes (ms). Inversement, la limite supérieure est d’environ 5 à 6 secondes, limite fixée par nos capacités à intégrer de manière hiérarchique les événements successifs dans un schéma stable » ([23], p. 27)13.
Et selon Paul Fraisse, plus l’intervalle de temps entre deux sons est grand, plus le nombre d’éléments que nous pouvons percevoir en série est petit. Cela a comme conséquence que plus une structure est dense, moins elle nécessite une interprétation rapide pour préserver le contenu musical par unité de temps. Nous avons comparé nos résultats avec ceux de Westergaard, sur les tempos perceptibles liés aux durées globales des battements ([35]; reporté en [23], Table 2.1). Ces études portaient sur des battements simples (rythme égal). Nous sommes allés plus loin en examinant l’effet de la complexité rythmique sur la perception du tempo. Nos résultats nous ont permis de constater, par rapport à l’étude de London, que des rythmes inégaux ou complexes (Scarlatti K. 450 et K. 238) entraînent une perception où la fourchette de tolérance – c’est-à-dire, la région entre les jugements « lent, mais acceptable » et « rapide, mais acceptable » qui correspondent aux valeurs numériques -1 et 1 sur l’axe vertical de la figure 4 – est beaucoup plus précise que lorsque les rythmes sont égaux (Scarlatti K. 25 et Prélude de Couperin).
Cela conduit à nous interroger sur les raisons pouvant expliquer l’influence de la structure rythmique sous-jacente. La tendance observée est que cette influence se produit bel et bien, mais dans une proportion inverse aux deux paramètres impliqués dans sa définition – c’est à dire, la variabilité dans la durée des notes et l’effet des syncopes) : si d’une part, la variabilité dans la durée des notes induit un feedback positif – déclenchant des tempos plus rapides – la présence de syncopes induit l’effet inverse – ce qui mène l’auditeur à préférer des tempos plus lents.
En ce qui concerne les structures mélodiques et harmoniques, les tendances à des corrélations (ou anti-corrélations) plus fortes concernent le registre mélodique, la taille moyenne des intervalles, leur direction moyenne, leur quantité (à la fois ascendante et descendante), et la tension harmonique résultant de l’effet combiné de la dissonance et du changement des accords. En comparant ces tendances avec celles trouvées par Quinn et Watt (2006), nous notons une tendance concordante pour l’écart-type de la durée des notes (malgré la valeur de corrélation, bien que statistiquement non significative, nous a semblé être beaucoup plus élevée). Mais notre étude diffère quant aux tendances pour la taille moyenne des intervalles, leur direction et leur quantité. L’interprétation que nous donnons à cela est la suivante. Contrairement à nous, Quinn et Watt (2006) ont trouvé une tendance à préférer des tempos plus rapides dans les pièces avec un plus grand nombre de notes. Dans notre répertoire, en fait, la densité des notes est à son tour lié à un aspect important de la structure rythmique – celui de la variabilité dans la durée des notes. Par conséquent, nous pensons que c’est la structure rythmique qui domine le tableau des corrélations, explicitement ou implicitement, en absorbant toutes les fluctuations qui peuvent être produites par d’autres facteurs. En d’autres termes, si dans notre cas une corrélation négative a été trouvée entre le tempo optimal et la quantité d’intervalles descendants, cela pourrait ne pas être lié à une question de perception mélodique, mais plutôt au fait que cette direction intervallique prévaut dans les morceaux avec des notes rythmiquement égales – une caractéristique qui a été à la fois démontrée être responsable d’une corrélation négative. Ceci est en partie conforme au résultat de Quinn et Watt (2006), selon lesquels la suppression de la structure mélodique par les extraits musicaux ne semblait pas empêcher les auditeurs de prendre des décisions sur la pertinence du tempo. Compte tenu de la grande différence des répertoires entre notre étude et la leur – musique baroque versus mélodies écossaises – cette conclusion semble reposer sur des principes plutôt généraux. Enfin, nous notons les fortes corrélations entre l’écart-type du tempo optimal et la tension de syncope, ainsi que entre l’écart-type du tempo optimal et le degré de dissonance : ces deux aspects, évidemment et intuitivement, tendent à confondre l’auditeur dans ses évaluations sur l’exactitude du tempo.
Afin de généraliser ces résultats, plusieurs ajouts à notre recherche seraient nécessaires. Bien que, comme il a été indiqué, il serait important de répéter les mesures de données sur un plus grand nombre d’extraits musicaux, il serait encore plus important d’étudier les effets produits sur le tempo optimal par des facteurs expressifs – en particulier ceux qui concernent les variations locales de tempo et leur vitesse d’action. Dans un autre article, nous avons étudié la relation entre les variations agogiques produites dans différentes interprétations du premier Prélude pour clavecin de François Couperin (le même utilisé dans cette étude, mais considérée dans son ensemble), et quelques-uns des paramètres structurels introduits ici, aboutissant à une classification des différentes interprétations expressives sur la base des accents mis sur certaines de ces structures [10]. Dans le futur, nous combinerons les résultats de celle et cette étude pour formuler une modélisation de l’effet de l’expressivité sur la détermination du tempo optimal.
Nous espérons que la mise en série des résultats de nos études, ainsi que la collecte de nouvelles données sur la perception du tempo effectuées sur de nouvelles interprétations d’un ou de plusieurs des morceaux choisis, nous amèneront à élargir notre vision sur le sujet fascinant que représente la perception du tempo dans la musique. C’est un domaine d’étude où la performance et l’éducation musicale peuvent également tirer profit. Dans le futur, il pourrait être aussi possible de calculer le tempo optimal par rapport à des indications usuelles telles que rapide, modéré ou lent. Cela s’avèrerait particulièrement intéressant dans le contexte de la musique baroque, une époque où les compositeurs ne pouvaient pas spécifier d’indications métronomiques sur la partition, puisque le métronome tel que nous le connaissons n’a été inventé qu’au XIXe siècle14. Même s’il ne sera pas possible d’abstraire complètement les questions de style et la tradition des ornements improvisés, nos résultats s’avèrent utiles pour faire une première approximation.
6. Bibliographie
[1] Auhagen, Wolfgang, « Preferred tempi of imagined compositions », dans Reinhard Kopiez, Andreas Lehmann, Irving Wolther, et Christian Wolf (dir.), Proceedings of the 5th Triennial ESCOM Conference, Hanover, Allemagne, Hanover, Université de musique et de théâtre, 2003, p. 639-642.
[2] Bisesi, Erica, Friberg, Anders et Parncutt, Richard, « A computational model of accent salience in tonal music », Frontiers in Psychology – Section Performance Science, vol. 10, no 317, 2019, p. 1-19.
[3] Bisesi, Erica et Parncutt, Richard, « An accent-based approach to automatic rendering of piano performance: Preliminary auditory evaluation », Archives of Acoustics, vol. 36, no 2, 2011, p. 283-296.
[4] Bisesi, Erica et Vicario, Giovanni Bruno, « The perception of an optimal tempo. The role of melodic event density », dans Alessandra Galmonte et Rossana Actis-Grosso (dir.), Different psychological perspectives on cognitive processes: Current research trends in Alps-Adria region, Cambridge, Cambridge Scholars Publishing, 2015, p. 25-43.
[5] Bisesi, Erica et Vicario, Giovanni Bruno, « Factors affecting the choice of performed tempo », British Postgraduate Musicology, vol. 10, 2009, p. 1-10.
[6] Boltz, Marylin Gail, « Tempo discrimination of musical patterns: Effects due to pitch and rhythmic structure », Perception & Psychophysics, vol. 60, 1998, p. 1357-1373.
[7] Bozzi, Paolo, Fisica ingenua, Milan, Garzanti Libri, 1998.
[8] Bregman, Albert Stanley, « Auditory scene analysis: The perceptual organization of sound », Cambridge MA, MIT Press, 1990.
[9] Caprin, Claudia, La natura delle alterazioni del tempo nella schizofrenia: Una analisi sperimentale, thèse, Université de Padoue, 1995.
[10] Caron, Sylvain, Bisesi, Erica et Traube, Caroline, « Analyser l'interprétation : Une étude comparative des variations de tempo dans le premier prélude de L'Art de toucher le clavecin de François Couperin », dans Philippe Lalitte (dir.), Musique et Cognition. Perspectives pour l’analyse et la performance musicales, Éditions Universitaires de Dijon, 2019, p. 233-266.
[11] Couperin, François, L’art de toucher le clavecin, Paris, Chés l’Auteur, le Sieur Foucaut, 1716, p. 52, téléchargé depuis le site web IMSLP le 26 mars 2015 : http://ks.petruccimusiclibrary.org/files/imglnks/usimg/2/21/IMSLP302585-PMLP09374-Couperin_-_L’art_de_toucher_le_clavecin_-1716-.pdf
[12] Desain, Peter et Honing, Henkjan, « Does expressive timing in music performance scale proportionally with tempo? », Psychological Research, vol. 56, 1994, p. 285-292.
[13] Fraisse, Paul, Psychologie du rythme, Paris, Presses Universitaires de France, 1974.
[14] Friberg, Anders, Bresin, Roberto et Sundberg, Johan, « Overview of the KTH rule system for musical performance », Advances in Cognitive Psychology, vol. 2, no 2-3, 2006, p. 145-161.
[15] Friberg, Anders et Bisesi, Erica, « Using computational models of music performance to model stylistic variations », dans Dorottya Fabian, Emery Schubert et Renee Timmers, (dir.), Expressiveness in music performance: Empirical approaches across styles and cultures, Oxford, Oxford University Press, 2014, p. 240-259.
[16] Fuller, David, « François Couperin révolutionnaire: Les pièces de clavecin », dans Catherine Cessac (dir.), François Couperin (1668-1733), Versailles, Éditions du Centre de musique baroque de Versailles, 2000, disponible en téléchargement : CMBV-2000-François Couperin révolutionnaire.pdf, http://philidor.cmbv.fr/content/download/492178/5308978/file/CMBV-2000-Fran%C3%A7ois%20Couperin%20r%C3%A9volutionnaire.pdf
[17] Herlin, Denis, préface au Premier livre des pièces de clavecins de François Couperin, Kassel, Allemagne, Bärenreiter, 2016, p. 14-15, https://www.amazon.it/clavecin-Cembalo-Premier-Spielpartitur-Urtextausgabe/dp/0006505619
[18] Kenneth, Gilbert, Domenico Scarlatti : Sonates, vol. 1, Paris, Heugel, 1984, p. 76-79.
[19] Kenneth, Gilbert, Domenico Scarlatti : Sonates, vol. 5, Paris, Heugel, 1974, p. 139-141.
[20] Kenneth, Gilbert, Domenico Scarlatti : Sonates, vol. 9, Paris, Heugel, 1972, p. 160-163.
[21] Lapidaki, Eleni, « Stability of tempo perception in music listening », Music Education Research, vol. 2, no 1, 2000, p. 25-44.
[22] LeBlanc, Albert, Colman, James, McCrary, Jan, Sherrill, Carolyn et Malin, Sue, « Tempo preferences of different age music listeners », Journal of Research in Music Education, vol. 36, no 3, 1988, p. 156-168.
[23] London, Justin, « Hearing in Time: Psychological aspects of musical metre », New York, Oxford University Press USA, 2004.
[24] London, Justin, « Rhythm », dans John Tyrrel et Stanley Sadie (dir.), The New Grove Dictionary of Music and Musicians, Oxford, Oxford University Press, vol. 21, 2001, p. 277-309.
[25] Moelants, Dirk et McKinney, Martin Franciscus, « Tempo perception and musical content: What makes a piece fast, slow or temporally ambiguous? », dans Scott David Lipscomb, Richard Ashley, Robert Gjerdingen et Peter Webster (dir.), Proceedings of the 8th International Conference on Music Perception and Cognition, Adelaide, Australie, Causal Productions, 2004, p. 558-562.
[26] Parncutt, Richard, « Accents and expression in piano performance », dans Klaus Wolfgang Niemöller (dir.), Perspektiven und Methoden einer Systemischen Musikwissenschaft, Francfort-sur-le-Main, Allemagne, Peter Lang, 2003, p. 163-185.
[27] Piston, Walter, « Harmony, 5ème Édition », révisée par Mark De Voto, New York, États-Unis, Norton, 1987.
[28] Quinn, Sandra et Watt, Roger, « The perception of tempo in music », Perception, vol. 35, no 2, 2006, p. 267-280.
[29] Quinn, Sandra Crouse et Watt, Roger, « Tempo judgements for music », dans Scott David Lipscomb, Richard Ashley, Robert Gjerdingen et Peter Webster (dir.), Proceedings of the 8th International Conference on Music Perception and Cognition, Adelaide, Australie, Causal Productions, 2004, p. 458-461.
[30] Repp, Bruno Hermann, « On determining the basic tempo of an expressive music performance », Psychology of Music, vol. 22, 1994b, p. 157-167.
[31] Repp, Bruno Hermann, « Relational invariance of expressive microstructure across global tempo changes in music performance: An exploratory study », Psychological Research / Psychologische Forschung, vol. 56, no 2, 1994a, p. 269-284.
[32] Strauss, Sabine, Vitouch, Oliver, Ladinig, Olivia, Augustin, Dorothee, Carbon, Claus-Christian et Leder, Helmut, « Memory rep¬resentations of musical tempo: Stable or adaptive? », dans Mario Baroni, Anna Rita Addessi, Roberto Caterina et Marco Costa (dir.), Proceedings of the 9th International Conference on Music Perception and Cognition, Bologne, Italie, Bononia University Press, 2006, p. 90-94.
[33] Umemura, Hiroyuki et Watanabe, Hiroshi, « Change in speed of movements affects interpretation of motion in 3-D scene », dans Abstracts of the 32th Conference on Visual Perception, supplément au Perception, vol. 38, 2009, p. 133.
[34] Wertheimer, Max, « Experimentelle Studien über das Sehen von Bewegung », traduit dans Thorne Shipley (dir.), Classics in psychology, New York, Philosophical Library, 1912/1961, p. 1032-1089.
[35] Westergaard, Peter, « An introduction to tonal theory», New York, W.W. Norton, 1975.
7. Notes
1. Le répertoire dont nous parlons correspond à celui de la common practice, tel que défini dans des ouvrages de musicologie théorique comme « Harmony » de Walter Piston [27], qui désigne ce qui correspond aux standards de la musique tonale, donc entre 1650 et 1900 environ. Le terme est toujours en usage, comme en témoigne l’article « Rhythm » de Justin London dans le Grove Music Online [24]. En plus, notre étude se limite à des musiques dont l’interprétation est conforme à la partition, ce qui exclut les pratiques d’improvisation qui ont cours dans certaines musiques baroques (notamment pour la basse continue).
2. « auditive streaming »
3. https://musescore.com/
4. Director Musices est un logiciel développé par l’équipe de recherche du département « Speech, Music and Hearing » à l’Institut Royal de Technologie (KTH) de Stockholm, qui automatise la production d’une interprétation expressive [14].
5. Fichiers disponibles ici
6. Même dans une danse, chez Couperin, le tempo n’est pas réglé selon une norme précise. Dans son article intitulé « François Couperin révolutionnaire: Les pièces de clavecin » ([16], p. 48], David Fuller explique que Couperin a précisément voulu affranchir les mouvements de la suite de la « tyrannie de la danse ».
7. Conformément à la déclaration d’Helsinki concernant les principes éthiques pour la recherche médicale impliquant des sujets humains.
8. https://www.finalemusic.com/
9. https://www.garritan.com/products/personal-orchestra-5/
10. Fichiers disponibles ici
11. Modèle ANOVA
12. Pour une interprétation du tableau 4, plus les valeurs des corrélations entre deux facteurs sont proches de 1, plus le lien entre eux est fort. Les valeurs négatives indiquent des anti-corrélations (valeurs dissociées), ou des liens inverses.
13. « Not all periodic stimuli afford entrainment – some are too fast, and others are too slow. Rapidly blinking lights can become a blur, and slowly (but regularly) dripping faucets will defeat our attempts to predict when the next drip will fall… The lower limit for meter, that is, the shortest interval that we can hear or perform as an element of rhythmic figure, is about 100 milliseconds (ms). Conversely, the upper limit is around 5 to 6 seconds, a limit set by our capacities to hierarchically integrate successive events into a stable pattern » ([23], p. 27).
14. La portée de notre étude se limite aux musiques où l’interprétation reproduit textuellement la partition. Les musiques françaises pour luth ou pour clavier du XVIIe siècle, ou encore les musiques baroques italiennes comprennent une part d’improvisation qui échappe à notre étude. Toutefois, dès le XVIIIe siècle, avec l’apparition des tables d’agréments, la plupart des compositeurs, comme Couperin ou Bach, demandent explicitement le respect de la partition écrite. En musique baroque française, la question des notes inégales peut toutefois avoir un effet sur l’interprétation ; notre étude ne se penche pas sur cette question.
